MWI – Alhamdulillah awal tahun 2021 ini dapat kembali berpartisipasi dalam lomba yang diadakan salah Universitas Islam Negeri di Indonesia, lomba kali ini terasa spesial karena lomba yang sebelumnya dilaksanakan di kampus dengan peserta data dari berbagai penjuru Indonesia, kali ini dilaksanakan secara daring (online).
Mulai dari proses izin untuk mengikuti lomba sampai dengan tahap pelaksanaan lomba yang memang kali ini terasa lebih spesial hingga pengisian link pendaftaran yang tak dapat diisi dengan huruf kami temui dalam pelaksanaan kali ini. Terima kasih kepada abun dan ananda sekalian yang tetap berjuang melakukan yang terbaik yang dapat dikerjakan.
Kali ini team ananda (kami) berhasil sampai dengan lomba di Tahap 3, ternyata ada soal yang menurut kami ada sedikit perbedaan, karena nilai ananda 0, berikut soal dan jawaban ananda, serta hasil searching kami terkait soal tersebut. Bagi kami ini adalah pembeljar yang luaar biasa untuk kami dan ananda. Terima kasih kakak panitia, guru pembimbing, ayah bunda (abun) sekalian dan ananda yang sudah berjuang luar biasa. Tetap semangat.
Daftar Isi
Soal dan Jawaban
Soal: (seingat dan sepemahaman ananda) Hitunglah berapa banyak cara dalam mengambil empat bilangan tidak berurutan dari himpunan {1,2,3,…,10}?
Jawab:

Jawaban diatas ternyata dianggap salah dan mendapatkan nilai 0 dari maksimal nilai 4 (jika dianggap benar dengan cara yang benar).
Berbekal rasa penasaran yang sangat, akhirnya melakukan pencarian (searching) kesana kemari untuk mendapatkan secercah harapan, berikut hasil pencarian yang didapat:
Hasil Pencarian 1 – Brainly
Di web Brainly ada pertanyaan seperti ini: Link Brainly
Cara memilih 4 bilangan dari 1,2,3…,10 dengan tidak ada yg berurutan ada sebanyak…
Pelajaran :Matematika
Kelas :9
Bab :6
Nama Bab :Barisan dan Deret Bilangan
Kode mapel:2
Kode :9.2.6
Jawab:
n(bilangan)=10
4C10=10!/4!(10-4)!
=10×9×8×7×6!/4×3×2(6!)
=10×9×8×7/4×3×2
=90×56/24
=5040/24
=210 cara
Namun jawaban ini disalahkan oleh penanya karena: Pilihan nya tak ada kak. A. 24. B. 35. C. 60. D. 72 dan E. 120. Karena dia tak beraturan
Hasil Pencarian 2 – Math StackExchange
Karena masih penasaran lanjut pencarian ke ranah internasional dan mendapat link jawaban pada forum matematika Stack Exchange dengan persoalan yang sama persis dan jawaban juga sama (35) tapi sipenanya penasaran kenapa hasilnya 35, berikut link Math StackExchange.
Soal: In how many ways can we choose 4 different numbers from the set 1,2,3,…,8,9,10
I did this question using PIE and I’m confused as to why I’m not getting the right answer. My approach: Use complementary counting. There are (104) ways to choose 4 different numbers. I then subtracted 9⋅(82) because there are 9 ways to choose the pair of numbers and then (82) ways to choose the last two numbers. I then added 8⋅(81) because I subtracted this case twice and thus have to add it in once. I then subtracted 7. I got a final answer of 7, but the correct answer is 35. What did I do wrong?
Jawaban1:
It looks like you applied the Inclusion-Exclusion Principle to cases with two consecutive, three consecutive, and four consecutive numbers. However, you should instead apply the Inclusion-Exclusion Principle to pairs of consecutive numbers.
There are (104) ways to choose four numbers from the set {1,2,3,4,5,6,7,8,9,10}
A pair of consecutive numbers: Your count is correct. The smaller of the two consecutive numbers must occur in one of the first nine positions. Choosing the smaller also determines the larger. The remaining two numbers can be selected in (82) ways, so there are (91)(82)
such selections.
Two pairs of consecutive numbers: This can occur in two ways. The pairs can overlap, or they are disjoint.
Two overlapping pairs: This means that three consecutive numbers are selected. Since the smallest of these three consecutive numbers must occur in one of the first eight positions. That leaves seven choices for the remaining number. Hence, there are (81)(71)
Two disjoint pairs: We have eight available positions, two for the pairs and six for the other six numbers. Choose two of the eight positions for the pairs. Doing so determines the pairs. For instance, if we choose the third and fifth positions, then the pairs are 3,4 and 6,7. 1,2,3,4,5,6,7,8,9,10 Hence, there are (82)
Three pairs: Since we are only selecting four numbers, this can only occur if we have four consecutive numbers. The smallest of these numbers can be selected in seven ways. Hence, there are (71)
By the Inclusion-Exclusion Principle, the number of ways four numbers can be selected from the set {1,2,3,4,5,6,7,8,9,10} such that no two consecutive numbers are selected is (104)−(91)(82)+(81)(71)+(82)−(71)
Jawaban2:
As an alternative method, imagine 6 stars in a row (the non chosen numbers), and among them place 4 bars in locations chosen from the 7 gaps in between or outside of the 6 stars. Now you have 10 objects in a row and the 4
bar locations correspond to the numbers you have chosen.
Convince yourself that there is a 1-1 correspondence between these star-bar things and the sets of 4
numbers you want.
The total number of them is the number of ways to choose 4 spots from a set of 7 spots i.e. C(7,4)=35.
Hasil Pencarian 3 – Math StackExchange
Berbekal dari link ke-2 akhirnya didapat pertanyaan mendasar tentang persoalan yang mirip (beda angka), dan ini saya kira yang pas untuk dijadikan acuan, link Math StackExchange
ini pertanyaannya: Choosing numbers without consecutive numbers.
In how many ways can we choose r numbers from {1,2,3,…,n}, In a way where we have no consecutive numbers in the set? (like 1,2)
Assuming that the order of choice doesn’t matter, imagine marking the positions of the r chosen numbers and leaving blank spaces before, between, and after them for the n−r non-chosen numbers; if r=3, for instance, you’d get a skeleton like _|_|_|_, where the vertical bars represent the positions in 1,2,…,n of the chosen numbers. The remaining n−r numbers must go into the r+1 open slots in the diagram, and there must be at least one of them in each of the r−1 slots in the middle. After placing one number in each of those slots, we have n−r−(r−1)=n−2r+1 numbers left to place arbitrarily in the r+1
slots. This is a standard stars-and-bars problem: there are
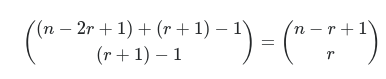
ways to do it. The reasoning behind the formula is reasonably clearly explained at the link.
Hasil Pencarian 4 – YouTube
Karena masih penasaran, akhirnya pencarian diarahkan ke situs dengan isi video dan didapatkan hasil yang sama dengan sebelumnya.
Soal: There are 10 points in a row. In how many ways can 4 points be selected such that no two of them are consecutive?
Jawab:
Update – Nilai Diubah
Setelah mengajukan komplain untuk soal 4 akhirnya ada pemberitahuan dari panitia, kalau nilai untuk soal no.4 diubah yang tadinya mendapat nilai 0 menjadi nilai 4, namun ternyata di nomor lain ada pengurangan untuk team kami nilainya dari 3 menjadi 1, dan sayangnya tidak ada meknisme resmi yang mengizinkan kami untuk melakukan komplain kembali. Terima kasih panitia sudah mendengarkan komplain kami, meski tetap mengusahakan agar hasil yang keluar sama.
Demikian sedikit catatan mengenai kegiatan anak-anak yang membuat penasaran orangtua-nya, sehingga munculah artikel ini. Ini hanya menjadi catatan bagi saya sebgai orangtua, bisa jadi memang ada kesalahan soal, atau bisa juag kesalahan memahami soal. Semoga bermanfaat, dan terima kasih. (ms).
Link:
1. Brainly
2. Math StackExchange
3. Math StackExchange
4. Wikipedia Star and Bar